Central Processing Unit vs Graphics Processing Unit
On entend souvent parler de GPU, mais qu’ont-ils de si particulier par rapport à des processeurs classiques comme les CPU ?
Nous sommes en 2026, alors pourquoi ne pas poser la question à un LLM? Voici la réponse de Claude Opus 4.5:
—— début de la réponse de Claude Opus 4.5 ——
Différence entre CPU et GPU
| Caractéristique | CPU | GPU |
|---|---|---|
| Nom complet | Central Processing Unit | Graphics Processing Unit |
| Architecture | Quelques cœurs puissants (4-64) | Milliers de petits cœurs (des milliers) |
| Optimisation | Tâches séquentielles | Tâches parallèles |
| Latence | Faible (rapide par tâche) | Plus élevée |
| Débit | Modéré | Très élevé |
Analogie simple
- CPU = Un professeur expert qui résout des problèmes complexes un par un, très rapidement.
- GPU = Une armée d’étudiants qui résolvent des milliers de problèmes simples simultanément.
Cas d’utilisation
CPU (cerveau généraliste) : - Système d’exploitation - Applications bureautiques - Logique complexe et décisions - Calculs avec dépendances séquentielles
GPU (spécialiste du parallélisme) : - Rendu graphique / jeux vidéo - Intelligence artificielle / Deep Learning - Minage de cryptomonnaies - Simulations scientifiques
Détails techniques
Architecture CPU
- Grande mémoire cache (\(L1\), \(L2\), \(L3\))
- Prédiction de branchement avancée
- Exécution spéculative
- Optimisé pour la latence
Architecture GPU
- Mémoire à haute bande passante (HBM, GDDR)
- Milliers d’unités de calcul (CUDA cores, Stream processors)
- Optimisé pour le throughput
- Modèle SIMD/SIMT (même instruction sur plusieurs données)
En résumé : Le CPU excelle dans les tâches complexes et variées, tandis que le GPU domine quand il faut effectuer la même opération sur d’énormes quantités de données en parallèle.
—— fin de la réponse de Claude Opus 4.5 (avec le doublon “milliers” laissé tel quel 🐱) ——
Ce qui resssort de cette réponse, c’est le côté généraliste vs spécialiste, et petite quantité vs grande quantité. L’image avec le professeur est très illustrative, et effectivement si on demande à un mathématicien d’effectuer 1 million de multiplications d’entiers compris entre 1 et 10 il va y arriver (la tâche est simple) mais cela va mettre du temps. Au contraire si on alloue à un million de personnes ce calcul, on peut espérer recevoir l’ensemble des réponses très rapidement.
Concrètement, ça se passe comment ? Voyons cela avec des exemples.
Du vecteur au tenseur : la puissance du parallélisme
Produit scalaire entre vecteurs
Pour illustrer le calcul en parallèle, prenons le produit scalaire entre deux vecteurs de dimension \(n\). Ce produit scalaire va s’obtenir en multipliant les coefficients de chacun de deux vecteurs deux à deux, puis en sommant le tout, au total \(n\) multiplications \(+ (n-1)\) additions soit \(2n - 1\) opérations.
Nous allons effectuer ce calcul en utilisant un CPU et un GPU, et observer la différence. Voici le code en Python:
import torch
import time
def compare_cpu_gpu_vectors(size:int)-> dict:
# CPU time
A_cpu = torch.rand(size)
B_cpu = torch.rand(size)
start_cpu = time.time()
C_cpu = torch.matmul(A_cpu, B_cpu)
end_cpu = time.time()
# GPU time
A_gpu = torch.rand(size).cuda() # <- note the .cuda()
B_gpu = torch.rand(size).cuda() # <- note the .cuda()
start_gpu = time.time()
C_gpu = torch.matmul(A_gpu, B_gpu)
torch.cuda.synchronize()
end_gpu = time.time()
time_cpu = end_cpu - start_cpu
time_gpu = end_gpu - start_gpu
ratio = time_cpu / time_gpu
result = {
"size": size,
"cpu_time": time_cpu,
"gpu_time": time_gpu,
"ratio": ratio
}
return resultEn lançant ce calcul pour size = 10’000’000 on obtient ces valeurs:
{'size': 10000000,
'cpu_time': 0.0066072940826416016,
'gpu_time': 0.0004439353942871094,
'ratio': 14.88345864661654}On observe que si on souhaite effectuer le produit scalaire de deux vecteurs de dix millions d’éléments chacun, le GPU sera environ 15 fois plus rapide que le CPU.
Traçons une courbe pour visualiser le ratio en fonction de la taille des vecteurs:
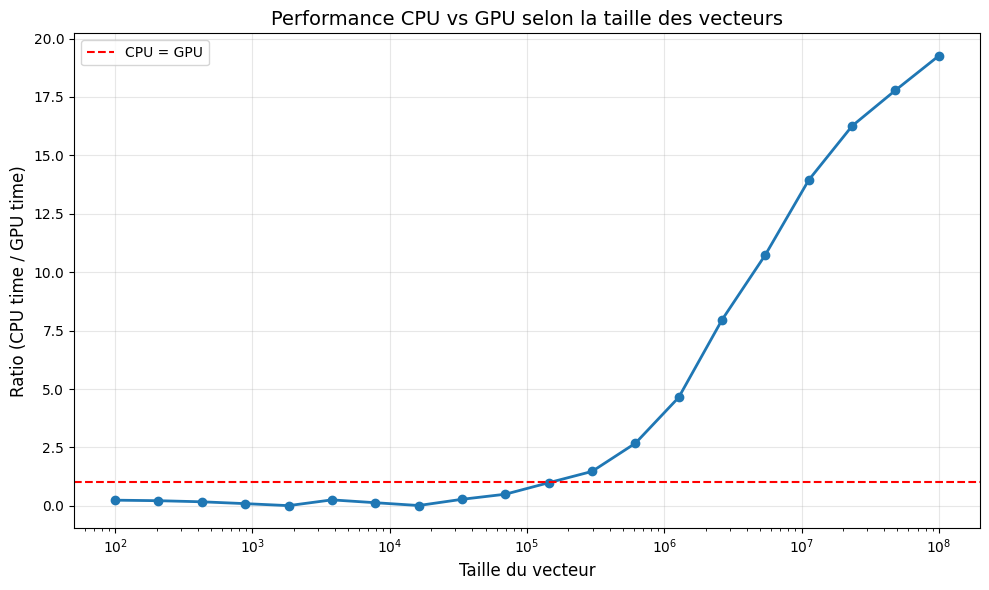
Il apparaît que pour des vecteurs de dimension inférieure à 100’000 le calcul avec un GPU prend un peu plus de temps que le calcul avec un CPU. Alors, le GPU n’est pas toujours le plus rapide ?? Cette apparente lenteur a une explication : avant de pouvoir alimenter les calculs du GPU, les nombres doivent être transférés du CPU au GPU. Cette écriture en mémoire prend du temps, pas beaucoup, mais suffisamment pour rendre l’utilisation d’un GPU moins rapide pour des calculs sur des vecteurs de “petite” dimension.
Multiplication de matrices
Passons à un autre exemple pratique : la multiplication matricielle. Prenons deux matrices carrées A et B de dimension n x n. Le produit de A par B est défini comme la matrice C dont les coefficients sont calculés… comme des produits scalaires entre les lignes de la matrice A et les colonnes de la matrice B, notés ainsi:
\[C_{ij} = \sum_{k=1}^{n} A_{ik} \cdot B_{kj}\]
Combien d’opérations seront nécessaires pour mener le calcul en suivant cette formule?
La matrice produit a \(n \times n = n^2\) éléments, et chaque élément étant un produit scalaire entre deux vecteurs de taille n nécessite \(2n - 1\) opérations, soit au total \(n \times n \times (2n - 1) \approx 2n^3\) opérations. On parlera d’une complexité \(O(n^3)\), là où le calcul du produit scalaire avait une complexité en \(O(n)\).
Sans spoiler la réponse cachée ci-dessous, on s’attend à ce que, les matrices de taille n x n étant plus “grandes” que les vecteurs de taille n, le calcul de leur produit nécessite plus d’opérations.
On adapte le code ci-dessus en ajoutant une dimension lors de la définition des variables A et B, qui deviennent ainsi des matrices:
import torch
import time
def compare_cpu_gpu_matrices(size:int)-> dict:
# CPU time
A_cpu = torch.rand(size, size) # <- we insert another dimension
B_cpu = torch.rand(size, size) # <- we insert another dimension
start_cpu = time.time()
C_cpu = torch.matmul(A_cpu, B_cpu)
end_cpu = time.time()
# GPU time
A_gpu = torch.rand(size, size).cuda() # <- we insert another dimension
B_gpu = torch.rand(size, size).cuda() # <- we insert another dimension
start_gpu = time.time()
C_gpu = torch.matmul(A_gpu, B_gpu)
torch.cuda.synchronize()
end_gpu = time.time()
time_cpu = end_cpu - start_cpu
time_gpu = end_gpu - start_gpu
ratio = time_cpu / time_gpu
result = {
"size": size,
"cpu_time": time_cpu,
"gpu_time": time_gpu,
"ratio": ratio
}
return resultOn lance le calcul pour size = 10’000’000 et on obtient…
Un plantage ! Une matrice 10’000’000 × 10’000’000 contient \(10^{14}\) éléments (100’000 milliards). En float32 (4 octets par nombre), cela représente 400 téraoctets de RAM rien que pour une matrice ! Il n’y avait AUCUNE chance que ça fonctionne, même sur les supercalculateurs les plus puissants.
Lançons le calcul avec size = 10’000, et voici les résultats:
{'size': 10000,
'cpu_time': 17.57096838951111,
'gpu_time': 0.6478822231292725,
'ratio': 27.12062125218268}On peut noter que le passage de vecteurs à des matrices a un impact considérable sur le temps de calcul, et que le ratio est largement en faveur du GPU.
Comme pour les produits scalaires, observons le ratio pour plusieurs valeurs de size:
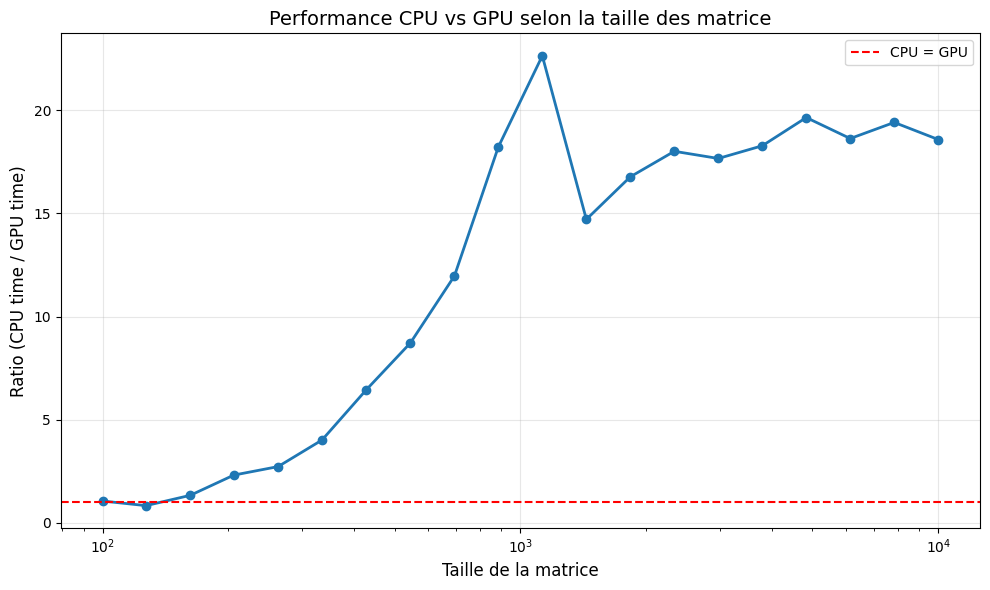
Trois observations:
- la taille de la matrice a été limitée à 10’000 × 10’000
- le processeur a été modifié (du T4 au A100 sur Google Colab)
- la courbe est moins régulière que celle du ratio pour les calculs de produits scalaires (problème de cold start ?)
Les tenseurs
Revenons aux vecteurs et aux matrices, pour essayer de les visualier comme l’extension d’un même objet. Un vecteur, au sens informatique, est une suite ordonnée de nombres, généralement écrit en ligne :
\[\begin{bmatrix} -2 & 1 & 3 & 0 & 2 \end{bmatrix}\]
ou en colonne :
\[\begin{bmatrix} -2 \\ 1 \\ 3 \\ 0 \\ 2 \end{bmatrix}\]
On va parler de vecteurs de taille n (par exemple ici un vecteur de taille 5), étant entendu que les éléments d’un vecteur tiennent sur une seule ligne (ou une seule colonne). La dimension d’un vecteur sera parfois notée (n, 1) par similude avec la notation utilisée pour les matrices.
Maintenant, nous pouvons visualiser une matrice comme étant un ensemble de vecteurs de même taille mis cote à cote, comme par exemple:
\[\begin{bmatrix} 1 & 6 & -2 \\ 7 & 2 & 9 \end{bmatrix}\]
On parlera d’une matrice de taille 2 x 3, pour 2 lignes et 3 colonnes. Cette fois-ci, contrairement au vecteur qui s’écrit sur un seul axe (ligne ou colonne), la matrice va s’écrire sur deux axes (ligne et colonne). On est passé d’un objet à 1 dimension (le vecteur), à un objet à 2 dimensions (la matrice).
Finalement, qu’est-ce qu’un tenseur ? Il va être l’extension à 3 dimensions et plus des vecteurs et des matrices.
Les tenseurs sont particulièrement utilisés dans la modélisation d’images en informatique: chaque image est un ensemble de pixels, de définition longeur x largeur. Mais cela ne fait que deux dimensions, pourquoi aurait-on besoin d’une troisième dimension (ou plus) ?
La troisième dimension permet de stocker trois variables R, G, B pour Red, Green, Blue, dont les valeurs sont comprises entre 0 et 255 et qui vont permettre de donner à chaque pixel une couleur.
Une image en noir et blanc quant à elle pourrait être modélisée par une matrice, dont les éléments seraient les niveaux de gris entre 0 et 255 de chaque pixel.
Le GPU n’est pas la solution à tous les problèmes
Quand le CPU reste le roi
Le GPU excelle dans le calcul parallèle, mais certaines tâches restent plus rapides sur CPU. Par exemple, les calculs avec logique conditionnelle :
def task_with_branching():
data = torch.rand(1000, 1000)
result = []
for i in range(1000):
if data[i, 0] > 0.5: # Branching
result.append(data[i].sum())
return resultLe GPU ne peut pas traiter efficacement ce type de code car tous ses cœurs doivent exécuter la même instruction. Les branchements (if/else) cassent le parallélisme.
Les limitations du GPU
Au-delà de la logique conditionnelle, d’autres situations favorisent le CPU :
- Petites données : l’overhead de transfert domine (< 100’000 éléments)
- Calculs séquentiels : boucles avec dépendances entre itérations
- Débogage : les messages d’erreur GPU sont souvent moins clairs
- Consommation énergétique : le GPU consomme significativement plus
L’optimisation logicielle avec JAX
Nous avons vu que les GPU excellent dans le calcul parallèle, notamment pour les opérations matricielles. Cependant, l’optimisation logicielle joue un rôle crucial dans les performances finales.
Prenons un exemple concret : calculer A @ B (une multiplication matricielle) versus A @ B + A @ B + A @ B + A @ B + A @ B (la même multiplication répétée 5 fois, puis additionnée).
Avec PyTorch, ces opérations sont exécutées séquentiellement : le GPU calcule A @ B, stocke le résultat, le recalcule, additionne, et ainsi de suite. Chaque opération nécessite des allers-retours en mémoire.
Avec JAX et sa compilation JIT (Just-In-Time), le compilateur XLA analyse l’ensemble des opérations et les fusionne : au lieu de 5 multiplications séparées, il optimise le calcul pour réduire les accès mémoire.
Le graphique ci-dessous montre l’impact spectaculaire de cette optimisation :
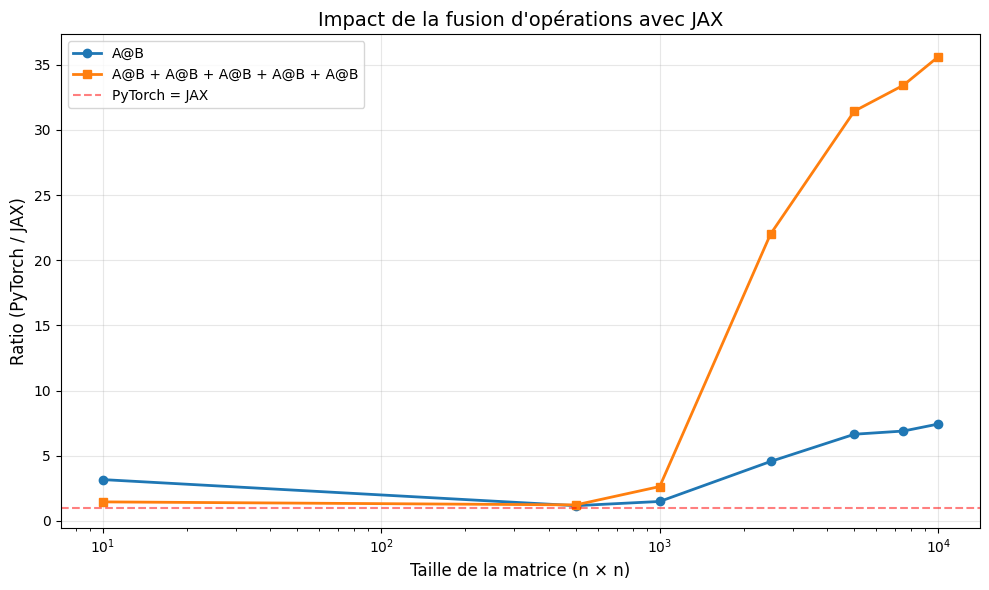
Pour les grandes matrices (10’000 × 10’000), JAX est jusqu’à 35 fois plus rapide que PyTorch sur les opérations répétées, contre seulement 7 fois sur une simple multiplication.
Le trade-off ? La première exécution avec JAX est plus lente (temps de compilation), mais toutes les exécutions suivantes bénéficient de l’optimisation.
Matériel
Cet article est le premier d’une série d’articles qui vont explorer les possibilités offertes par la vision par ordinateur ou computer vision.
Pour nous aider, nous aurons besoin de… CPU et GPU ! Voici les processeurs que nous aurons à notre disposition et un résumé de leurs caractéristiques:
| Caractéristique | iMac 2010 (Linux) | Raspberry Pi 5 (8Go) | RPi 5 + Hailo 8L | Jetson Orin Nano Super | Google Colab (T4/A100) |
|---|---|---|---|---|---|
| Architecture | x86-64 (Intel Nehalem) | ARMv8.2-A (Cortex-A76) | ARM + Dataflow (NPU) | ARM + Ampere (GPU) | x86-64 + NVIDIA GPU |
| CPU (Cœurs) | 2 à 4 cœurs physiques | 4 cœurs | 4 cœurs (Hôte) | 6 cœurs (Cortex-A78AE) | 2 à 12 vCPU (Intel Xeon) |
| Cadence (CPU) | 3.06 GHz - 3.6 GHz | 2.4 GHz | 2.4 GHz | Jusqu’à 1.5 GHz | 2.2 GHz - 2.9 GHz (Boost) |
| Mémoire (RAM) | 4 Go - 16 Go DDR3 | 8 Go LPDDR4X | 8 Go (Hôte) + SRAM interne | 8 Go LPDDR5 (Partagée) | 13 Go - 85 Go (High-RAM) |
| Accélérateur IA | Aucun (CPU pur) | Aucun (CPU pur) | NPU Hailo-8L | GPU Ampere (1024 cœurs) | NVIDIA T4, L4 ou A100 |
| Mémoire Vidéo (VRAM) | 256 Mo - 512 Mo | Partagée avec RAM | Mémoire interne (buffer SRAM) | Partagée avec RAM | 16 Go - 40 Go (HBM2) |
| Perf. IA (Inférence) | N/A | N/A | 13 TOPS (INT8) | 40 TOPS (INT8) | 65 - 624 TOPS (INT8) |
| Consommation | 150W - 250W | 3W - 12W | 5W - 15W | 7W - 15W | N/A (Cloud) |
| Prix approximatif | ~500€ (occasion) | ~90€ | ~160€ | ~250€ | Variable (crédits) |
| €/TOPS | N/A | N/A | ~12€ | ~6€ | Variable |
Conclusion
Dans cet article nous avons identifié ce qui distingue un CPU d’un GPU et illustré la différence de performances pour effectuer des calculs parallélisables.
Nous avons vu que :
- Le GPU excelle sur les grandes données : pour les opérations matricielles de grande taille, le GPU peut être 15 à 30 fois plus rapide qu’un CPU
- L’overhead mémoire compte : pour les petites données, le temps de transfert CPU→GPU peut annuler l’avantage du parallélisme
- L’optimisation logicielle est cruciale : avec JAX et la compilation JIT, on peut gagner jusqu’à 35x en performance par rapport à PyTorch sur des opérations enchaînées
- Le matériel se diversifie : CPU, GPU, NPU et TPU offrent différents compromis performance/consommation/coût
Dans les prochains articles de cette série, nous mettrons en pratique ces concepts avec de la computer vision : détection d’objets, classification d’images, et traitement vidéo en temps réel sur nos différentes plateformes.
Pour en savoir plus
💡 Glossaire technique
- CUDA : Architecture de calcul parallèle développée par NVIDIA
- HBM2 : High Bandwidth Memory, mémoire à très haute vitesse
- TOPS : Trillions d’Opérations Par Seconde (métriques d’IA)
- JIT : Just-In-Time compilation, compilation à la volée
- NPU : Neural Processing Unit, accélérateur dédié à l’IA
- TPU : Tensor Processing Unit, processeur spécialisé de Google