Nombres aléatoires et ordinateurs

Quand on entend parler de “nombres aléatoires” on peut penser à une suite de nombres dont il est impossible de savoir à l’avance quel sera le nombre suivant dans la série, par exemple, les tirages d’un dé. Les observations de nombres aléatoires sont indépendantes les unes des autres.

On n’y pense peut-être pas tout de suite, mais les suites de nombres aléatoires ont généralement une autre caractéristique, qui est que chaque nombre de la série suit une distribution identique. Pour reprendre l’exemple des tirages d’un dé, en plus d’être indépendants, les résultats du tirage vont être réalisés de la même manière, notamment les nombres seront pris parmi les nombres entiers compris entre 1 et 6, et uniquement les entiers entre 1 et 6.

Quel rapport avec les ordinateurs ? Les ordinateurs sont très efficaces pour conduire des opérations qui ont été clairement définies, et sont a priori déterministes. Toutefois, pour certaines applications, comme les jeux de roulette en ligne, les ordinateurs doivent pouvoir générer des nombres aléatoires. Comment l’ordinateur va-t-il déterminer le numéro gagnant?

Middle Square Method - Von Neumann

Pour générer un tirage aléatoire avec un dé, il suffit… de le faire rouler ! Le dé est fait pour cela, et le résultat du tirage est immédiat, c’est la raison d’être du dé.

Avec un ordinateur, c’est un peu différent: l’ordinateur a été créé pour effectuer des calculs, puis pour exécuter des algorithmes. Pas pour générer des nombres aléatoires, du moins pas dans le sens vraiment aléatoire. Alors comment fait un ordinateur pour simuler un tirage de jeu de roulette ?

L’approche va consister à créer des suites de nombres qui semblent aléatoires, même s’ils ne le sont pas. Pour cela il faudra que ces suites se comportent “bien” de manière statistique, notamment que les nombres de la suite soient indépendants les uns des autres, et qu’ils soient identiquement distribués (qu’ils suivent la même distribution de probabilité).

On va parler de générateurs de nombres pseudo-aléatoires. Il en existe plusieurs, commençons par la méthode du carré du milieu, proposée par John Von Neumann.

Voici comment fonctionne cet algorithme:

Initialisation: on part d’un nombre de départ appelée la graine (seed en anglais)
Elévation au carré: on multiplie ce nombre par lui-même
Formattage: on transforme le résultat en une chaîne de caractères de longueur fixe (par exemple 8 caractères) en ajoutant des zéros si nécessaire
Extraction: on récupère les chiffres situés au centre de cette chaîne (par exemple les 4 chiffres du milieu)
Ce nouveau nombre devient la graine pour le tour suivant et on recommence le processus

Nous allons illustrer cet algorithme (et les suivants) en simulant la génération d’un nombre aléatoire compris entre 0 et 36 comme pourrait le faire un jeu de roulette.

Voici le code en Python:

def roulette_v1_middle_square(seed=4798, nb_plays=15):
    """Middle Square Method - Von Neumann"""
    results = []
    current = seed
    
    for _ in range(nb_plays):
        squared = current ** 2
        # Extract middle 4 digits
        str_squared = str(squared).zfill(8)  # Pad with zeros
        middle = int(str_squared[2:6])
        results.append(middle % 37)
        current = middle
    
    return results

Maintenant, faisons tourner la roue et observons les résultats !

[23, 25, 16, 9, 7, 12, 11, 26, 2, 6, 27, 31, 32, 30, 12]

A première vue, tout se passe bien: les tirages obtenus sont bien compris entre 0 et 36 (heureusement!) et ne présentent pas d’ordre particulier ni de répétition.

Essayons de confirmer cela en réalisant 10’000 tirages et en affichant la distribution observée:

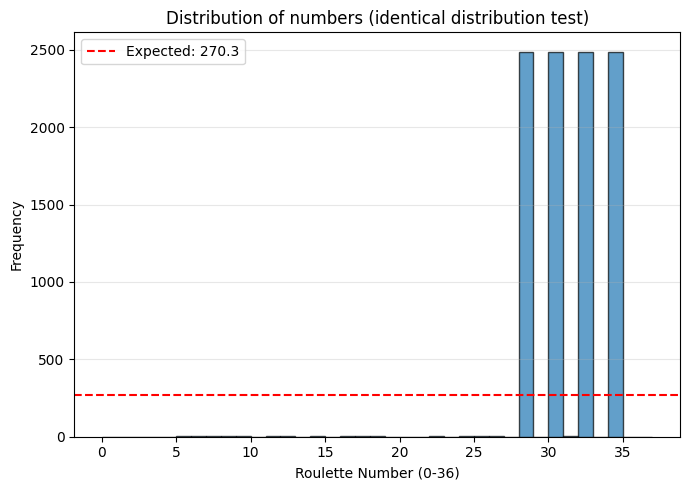
On est loin d’une distribution homogène !

Hm… il semble y avoir un problème ! A priori, chacun des nombres de la roulette a la même probabilité de sortie, aussi on devrait s’attendre à ce que chacun des nombres apparaisse environ autant de fois que les autres, sur un tirage de 10’000 nombres cela correspond à 10’000 / 37 soit environ 270 fois. Or on observe que les nombres 28, 30, 32 et 34 apparaissent beaucoup plus souvent que les autres.

Pourtant, tout semblait bien parti sur les 15 premiers tirages, alors que s’est-il passé entre temps…? Visualisons cela sur les 500 premiers tirages:

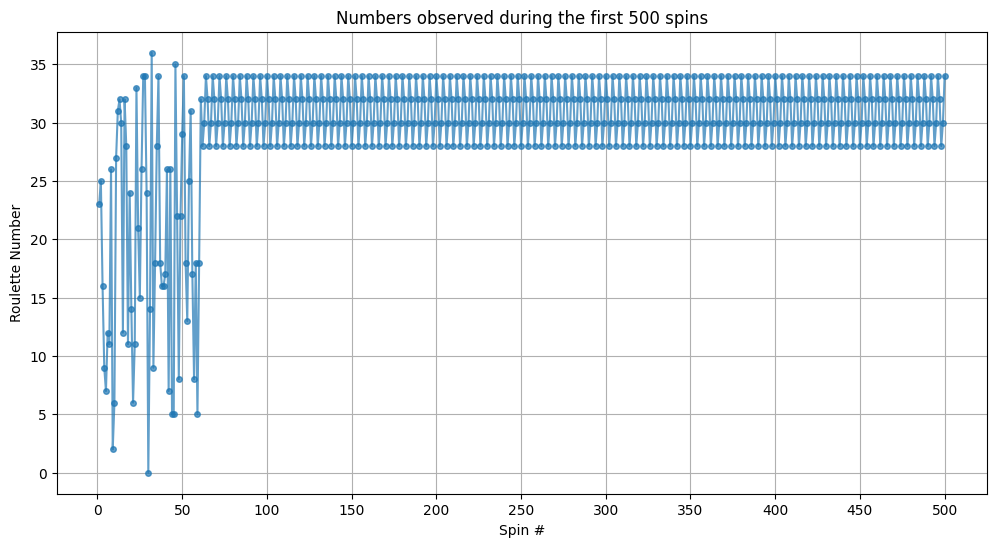
Voilà l’explication : à partir du tirage 61, l’algorithme va rentrer dans une séquence 32 \(\rightarrow\) 28 \(\rightarrow\) 30 \(\rightarrow\) 34 de laquelle il ne sortira pas… on peut continuer les tirages, seuls ces quatre nombres vont sortir, ce qui explique leur fréquence anormalement élevée dans la distribution.

Conclusion: pour un casino en ligne, utiliser cet algorithme c’est la ruine assurée !

Linear Congruential Generator

Testons un autre algorithme de génération de nombres aléatoires: le générateur congruentiel linéaire. C’est une méthode très populaire car elle est à la fois rapide et simple à implémenter. Elle repose sur une formule arithmétique précise plutôt que sur la manipulation de chiffres comme la méthode précédente.

Voici comment fonctionne l’algorithme:

Initialisation: comme toujours, on part d’une graine initiale (seed)
Calcul linéaire: on multiplie la graine par une constante a (le multiplicateur) et on ajoute une constante c (l’incrément)
Modulo: on calcule le reste de la division du résultat par un grand nombre m (le module), afin de limiter la taille du nombre et de créer l’effet pseudo-aléatoire
Itération: ce nouveau nombre devient la graine, et on recommence

La qualité de la génération va dépendre du choix des constantes a, c et m.

Utilisons cet algorithme en Python pour constituer un deuxième générateur de roulette:

def roulette_v2_lcg(seed=1234, nb_plays=15, a=517, c=23, m=2**11):
    """Linear Congruential Generator"""
    results = []
    current = seed
    
    for _ in range(nb_plays):
        current = (a * current + c) % m
        results.append(current % 37)
    
    return results

Comme pour le premier algorithme, faisons tourner la roue !

[0, 28, 0, 16, 2, 25, 35, 4, 29, 1, 2, 2, 8, 18, 26]

Les tirages semblent là aussi aléatoires… mais ne nous emballons pas trop vite, car comme nous l’avons vu précédemment une série de tirages aléatoires peut à la fois bien partir mais mal finir !

Réalisons 10’000 tirages et observons la distribution :

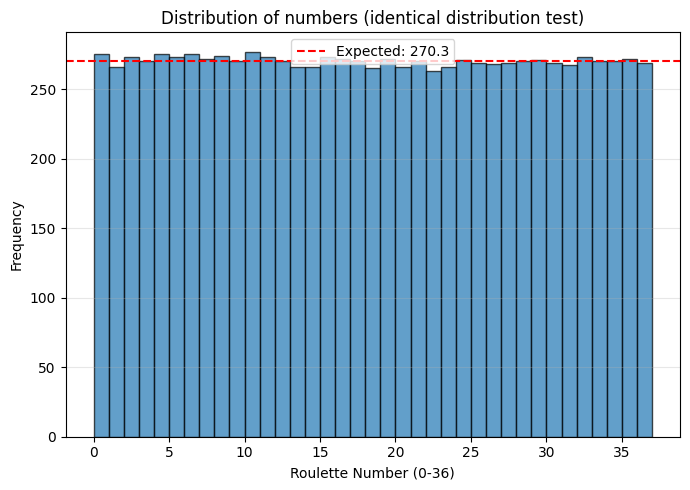
Le graphique montre des valeurs plutôt équitablement réparties, comme on pourrait s’attendre de la part de tirages aléatoires. Visualisons tout de même les valeurs obtenues pour les 500 premiers tirages:

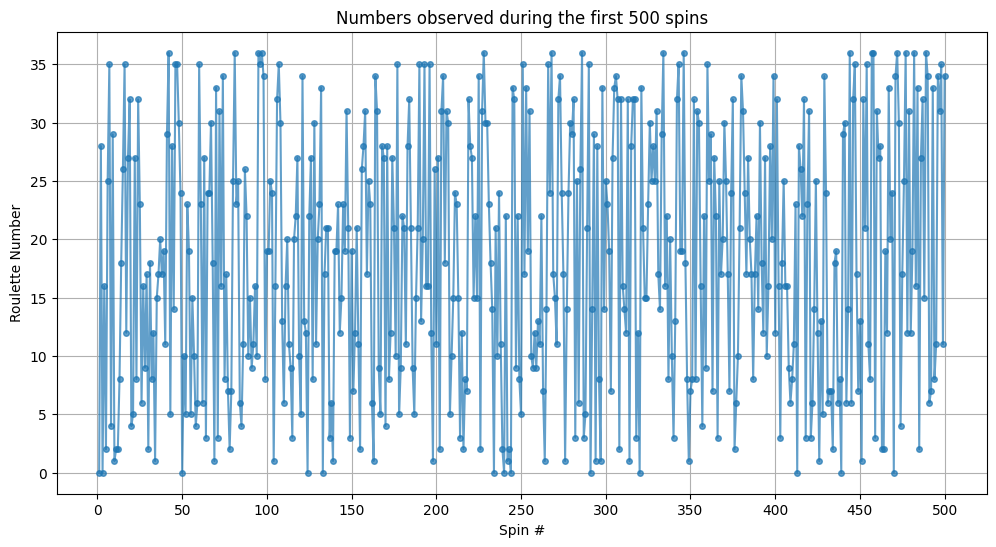
A première vue, nous n’avons plus le problème de boucle infinie observée avec le premier générateur. Les nombres semblent plutôt aléatoires même si… un doute peut apparaître sur une possible saisonalité. Si c’était le cas, l’indépendance entre les tirages pourrait être remise en cause.

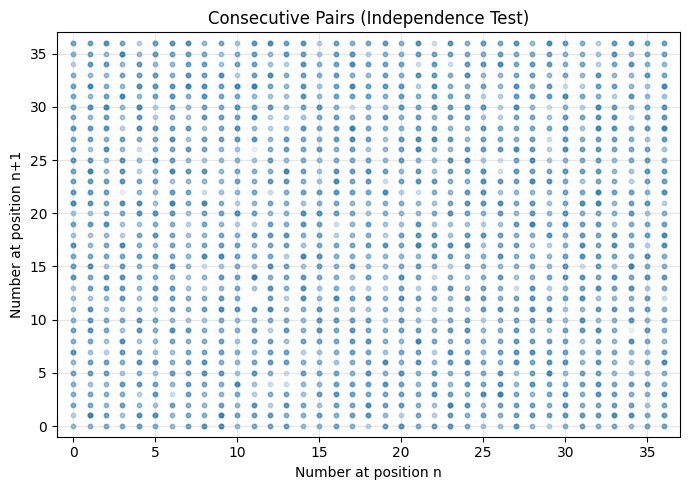
Essayons de tester cette possible saisonalité avec un nuage de points dont les coordonnées sont les paires des valeurs obtenuers pour deux tirages consécutifs:

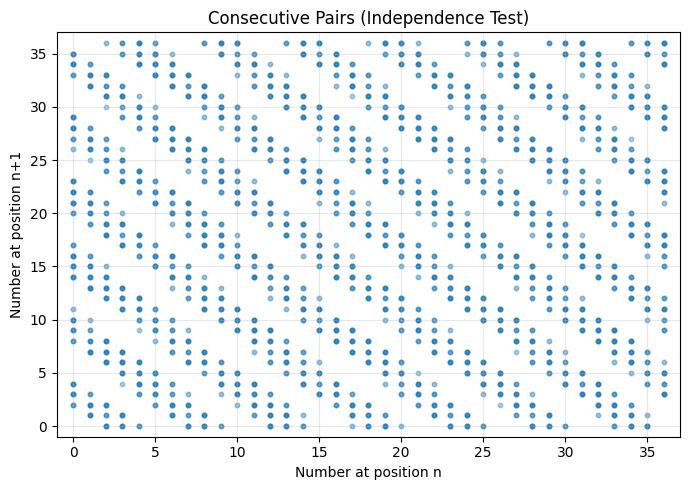
Avec une telle distribution, difficile d’admettre que les tirages sont indépendants les uns des autres. Là encore, scénario de ruine certaine pour un casino utilisant cet algorithme !

Enfin, cet algorithme… ou cet algorithme avec ces paramètres? Nous avons en effet retenu les valeurs suivantes: a=517, c=23, m=\(2^{11}\). Que se passe-t-il si on utilise a=1103515245, c=12345, m=\(2^{31}\) ? Ces valeurs ne sortent pas de nulle part : ce sont celles utilisées dans l’implémentation de référence de la fonction rand() définie par la norme ANSI C et le standard POSIX.

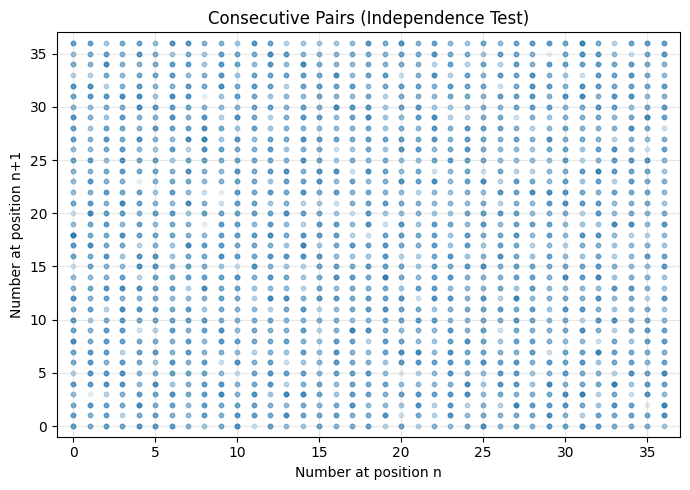
Avec ce nouveau triplé comme paramètres, l’algorithme produit une séquence de nombre pseudo-aléatoires qui semblent plus indépendants que précédemment.

Xorshift Generator

Terminons avec un troisième et dernier générateur de nombres pseudo-aléatoires: le générateur Xorshift. Contrairement aux méthodes précédentes qui utilisent des opérations sur la représentation décimale des nombres, le générateur Xorshift va opérer sur la représentation binaire, ce qui est souvent très rapide en temps de calcul.

Voici les étapes de l’algorithme:

Initialisation: on part d’une graine (seed)
Manipulation de bits: on travaille directement sur la représentation binaire (0 et 1) du nombre
Décalage et XOR: l’algorithme effectue trois opérations de décalage (gauche, droite, gauche) combinées à des “Ou Exclusif” (XOR). Cela mélange les bits de manière imprévisible
Masquage : on applique un masque (& 0xFFFFFFFF) pour forcer le nombre à rester sur 32 bits (nécessaire en Python pour simuler le comportement d’un processeur standard)

Et voici le code Python pour simuler un jeu de roulette en utilisant cet algorithme:

def roulette_v3_xorshift(seed=1234, nb_plays=15):
    """Xorshift Generator"""
    results = []
    current = seed
    
    for _ in range(nb_plays):
        current ^= (current << 13) & 0xFFFFFFFF
        current ^= (current >> 17)
        current ^= (current << 5) & 0xFFFFFFFF
        results.append(current % 37)
    
    return results

Pour la dernière fois, lançons la roulette !

[8, 23, 36, 29, 6, 10, 9, 29, 15, 9, 2, 14, 27, 19, 22]

Et observons les tirages:

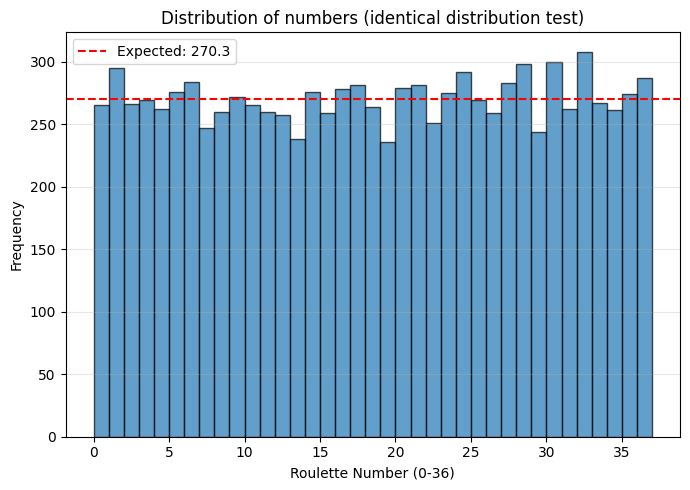
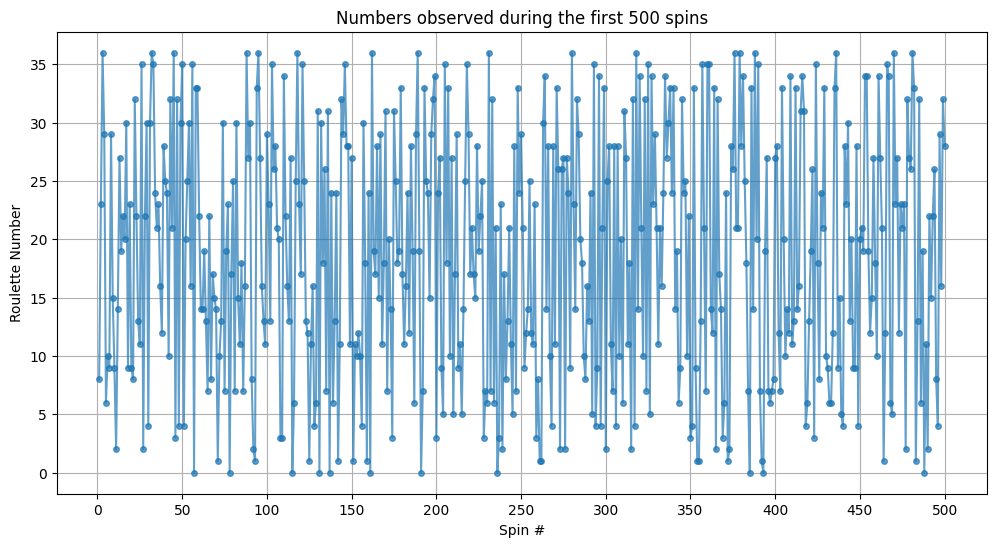
Cette fois-ci, c’est un sans faute ! La méthode n’est pas évidente au premier abord, mais elle est très efficace.

Conclusion

En voulant simuler un jeu de roulette, nous avons testé trois générateurs de nombres pseudo-aléatoires, et pouvons retenir ceci:

Pour qu’ils semblent aléatoires, les nombres générés doivent présenter deux caractéristiques : être indépendants les uns des autres et être identiquement distribués
Il existe différentes approches pour générer des nombres pseudo-aléatoires, allant du travail sur l’écriture du nombre à sa manipulation en représentation binaire en passant par des calculs de restes de divisions euclidiennes
Même si les nombres obtenus paraissent aléatoires, il est plus prudent de multiplier les tests notamment au moyen de représentations graphiques afin d’éviter de déchanter !
Ces générateurs sont tous… déterministes : même graine, même séquence ! C’est pourquoi, pour de la cryptographie (mots de passe, clés bancaires), on n’utilise jamais ces générateurs ‘simples’, mais des versions beaucoup plus complexes (CSPRNG).